What the model of human population growth means for the apocalypse

Environmentalists, social advocates, and apocalypse-aficionados all enjoy scaring the masses with the idea of the exponential growth of the human population.  At first glance, the dire warnings of overpopulation seem completely supported, given the explosion from 2.5 billion people in 1950 to more than 7 billion people today.  But is an exponential model, always increasing at an increasing rate (general form: dN/dt = rN), really representative of how we will expand?  Intuition says no.  There has to be a cap in our growth, right?  We cannot keep growing forever.  Scientists have been confident of self-limiting growth for centuries.  I, for one, like the idea of self-limiting growth, seeing as how the African driver ant queen lays between 3-4 million eggs every month.  But here’s the thing: those old-timey predictions of the stabilization of human population failed. A long time ago.  In fact, about 5 billion of us should not be here right now, if older predictions were correct.  Yet here we are, with roughly 6% of all humans ever born alive right now.  

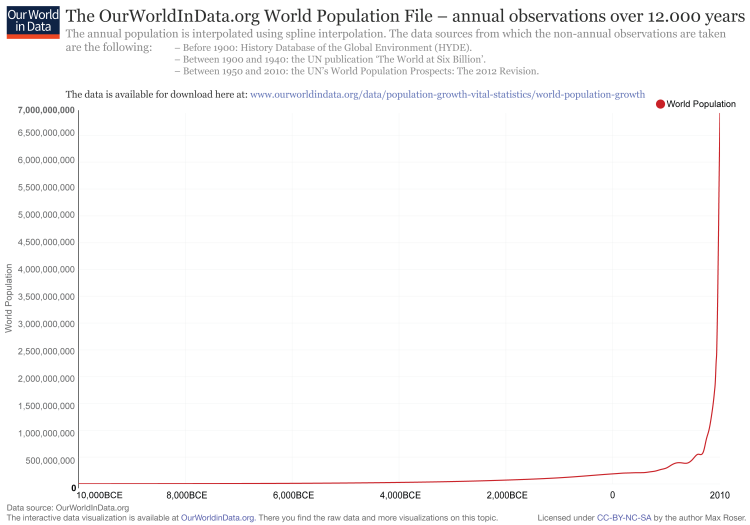
It sure looks exponential, doesn’t it? But a sharp curve does not mean the math fits.  A wonderful illustration of this is available from Math Bench. This tool allows you to find the best fit growth rate over distinct periods: early (up to 0 CE), mid (0 CE – 1950 CE), and modern (1950-present).

No exponential model fits that variation!  Technology, it seems, is ruining math.  Advances in food production and medicine (among other things) have allowed for steeper exponential growth in the modern era. 

Ok, you might be saying, so an exponential function might be able to fit if we just look at the post-Industrial Revolution age.  That should be all that matters, since we can’t really say that human civilization is anything like it was in the Bronze Age, right?  If you think so, you should be investing heavily in the Mars colony, because the carrying capacity of Earth will smack us in the face if we’re not careful.  The most cheerful estimates cap us off at 40 billion, and that is with every human being surviving with subsistence living (not to mention a civilization of vegetarians).  Good luck with that one, America.  If everyone on Earth lived like us, we’d have to get by with only 2 billion of our closest friends.

Enter the logistic model, or dN/dt=rN(1-N/K), where K is carrying capacity. With such divergent beliefs of the true carrying capacity of Earth (2 – 40 billion), any attempt at a logistic model starts off handicapped.  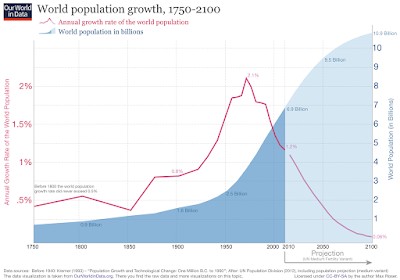Couple that with the fact that all logistic models have an inflection point somewhere (the point at which growth starts increasing at a decreasing rate), and the problems with fitting a logistic model multiply.  If we look only at the very recent past, we can squint and see that the inflection point has been passed (which is by definition at a population of K/2).

If we zoom out, that inflection point is hard to see:

The best-fit model seems to depend on our time frame.  All because technology screwed up the statistics.

What does that mean for us?  Without technological innovation, carrying capacity would likely be around 2 billion.  Remember that Mars mission you should be supporting?  If we go beyond Earth’s resources, carrying capacity could become irrelevant (at least in the short term). New worlds, or even just an influx of new resources (think about Ceres, possibly holding more freshwater than all of Earth) changes the game, and perhaps the model.  Without scarcity, there need not be an inflection point.  The more frightened we become of the impending apocalypse, the more innovative we will be.  In the contest between exponential and logistic functions to explain human population growth, every new extra-planetary mission is a point for the exponential model.